Error functions
The error function (also called the Gauss error function), often denoted by erf, is a function defined as
$$
\operatorname{erf} z = \frac{2}{\sqrt\pi}\int_0^z e^{-t^2}dt
$$
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
|
use mathru::special::error;
use plotters::prelude::*;
fn main() {
let x_start: f64 = -3.0;
let x_end: f64 = 3.0;
let length: usize = 2000;
let mut graph_1: Vec<(f64, f64)> = Vec::with_capacity(length);
for i in 0..length {
let x: f64 = (x_end - x_start) / (length as f64) * (i as f64) + x_start;
graph_1.push((x, error::erf(x)));
}
let root_area = BitMapBackend::new("./figures/erf.png", (600, 400)).into_drawing_area();
root_area.fill(&WHITE).unwrap();
let mut ctx = ChartBuilder::on(&root_area)
.margin(20)
.set_label_area_size(LabelAreaPosition::Left, 40)
.set_label_area_size(LabelAreaPosition::Bottom, 40)
.build_cartesian_2d(x_start..x_end, -1.1f64..1.1f64)
.unwrap();
ctx.configure_mesh()
.x_desc("x")
.y_desc("erf(y)")
.axis_desc_style(("sans-serif", 15).into_font())
.draw()
.unwrap();
ctx.draw_series(LineSeries::new(
graph_1,
Into::<ShapeStyle>::into(&BLUE).stroke_width(2),
))
.unwrap();
}
|
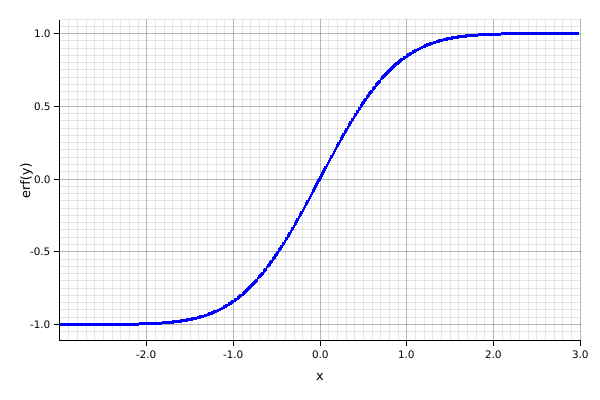
Complementary error function
$$
\operatorname{erfc}(z) = 1 - \operatorname{erf} z,
$$
